MRAS

MRAS

Dokument z 1987 roku.
Od lat szeroko stosuje sie analogowe a ostatnio cyfrowe regulatory PI oraz PID. Dla niezbyt trudnych obiektow regulacji - sterowania o niezbyt duzym opoznieniu faktycznie nie ma dla nich alternatywy. Do poprawnego nastrojenia regulatora na obiekcie potrzebny jest doświadczony personel. Nastrojenie regulatora jest czasochłonne i sporo kosztuje. Jest to trudne zadanie. Akademickiej metody Zieglera-Nicholsa raczej nie mozna stosowac bowiem duze zaburzenia procesu przemyslowego moze miec oplakane i kosztowne rezultaty. Astrom w 1984 roku zaproponowal automatyzacje eksperymentu Zieglera-Nicholsa z polepszeniem bezpieczenstwa. Oscylacje z obiektem wytwarza dwupolozeniowy regulator z histereza. Metoda jest wiec toporna.
Skutkiem tego 30-40 % zainstalowanych regulatorów pracuje w trybie sterowania ręcznego. Zas 25-30% regulatorow ma nastawy wybrane ze srodka zakresu czyli tak zwane nastawy fabryczne co prowadzi do prostego wniosku ze nikt nawet nie probowal ich nastroic. Prawie wszystkie powolne regulatory w trybie manualnym daja lepsze efekty niz w trybie automatycznym. Oczywiscie skutkiem ich nienastrojenia. Szczegolny niepokoj budzi wsrod operatorow praca automatyczna w czasie rozruchow gdzie duze przeregulowania skutkiem slabego panowania nad calkowaniem (wind - up czy lapanie wiatru w zagiel) moga byc niebezpieczne.

Czesc obiektow sterowania wykazuje znaczne zmiany w zachowaniu. Innaczej zachowuje sie samolot do pelna zatankowany z ladunkiem a innaczej bez paliwa i ladunku. Tak samo statek morski z pelnymi ladowaniami zachowuje sie odmiennie niz tylko z minimalnym balastem. W tych sytuacjach jednak samonastrajanie czy adaptacja sa zbedne bowiem informacja o zmianie dynamiki obiektu jest dostepna.

Rozwiazaniem jest idea samonastrajania - Self Tuning Regulator lub adaptacji. Praca magisterska autora poswiecona jest wlasnie komputerowej analizie takich dyskretnych systemow STR. Systemy maja zdolnosc uczenia sie zatem jest to pogranicze sztucznej inteligencji. STR nie sa jeszcze dopracowane na tyle aby wkroczyc do masowej produkcji.

Najprostsza idea Model Reference Adaptive System znana jest od poczatku lat szescdziesiatych z laboratoriow MIT. Usytematyzowano i rozwinieto ja znacznie. Wykorzystuje sie gradienty i funkcje wrazliwosci na parametry odpowiedzi dostrajanej transmitancji. "Laboratorium Teori Sterowania ", praca PS IAP, 1980 pod redakcja prof Adama Zuchowskiego na stronach 208-214 daje przyklad zastosowania tej idei do ukladu II rzedu gdzie dostrajane sa dwa parametry. Mankamentem jest znaczna komplikacja (schemat symulacyjny na stronie 213) i niezbyt dobre rezultaty dostrajania .
Wspolczesnie idea MRAC jest stosowana analogowo z czasem ciaglym i w realizacji cyfrowej z czasem dyskretnym.
Od klku lat znany jest nowoczesny ogolny sposob syntezy ukladu MRAS dla obiektow liniowych SISO korzystajacy z metody Lapunowa. Z reguly system jest prosty i zagwarantowana jest stabilnosc BIBO przy dowolnym wzmocnieniu petli adaptacji.
Znana jest analogia miedzy systemem ciaglym MRAS a systemem cyfrowym - dyskretnym STR Zawsze i w kazdym systemie aby zachodzila adaptacja wymagane sa zmiany sygnalu sterujacego.
Autor idee MRAS zastosowal do precyzyjnego dostrajania filtru srodkowozaporowego. Analiza matematyczna jest zlozona. Konieczna jest znajomosc filtru Kalmana i metod DSP.
Jak widac z symulacji filtr zawsze sie dostraja. Bardzo wysokiej jakosci generator sygnalu sinusoidalnego oraz taki filtr moga sluzyc do analizy znieksztalcen nieliniowych we wzmacniaczach, ukladach przetwarzania sygnalu i w doskonale rokujacych super przetwornikach A/D i D/A rodziny Sigma Delta o rozdzielczosci nawet 20 bitow.
Wstepnie obrobiony sygnal z usunieta sinusoida sygnalu testowego podaje sie do przetwornika A/D w komputerze PC i wylicza Spectrum z uzyciem FFT i odpowiedniego okna. Potencjalne mozliwosci metody przekraczaja wyobraznie !
Szybkosc procesu nastrojenia filtru zalezy oczywiscie od tego jak bardzo poczatkowe estymaty odbiegaja od ich prawdziwej wartosci. Stan poczatkowy filtru zmiennych stanu tez ma znaczenie.
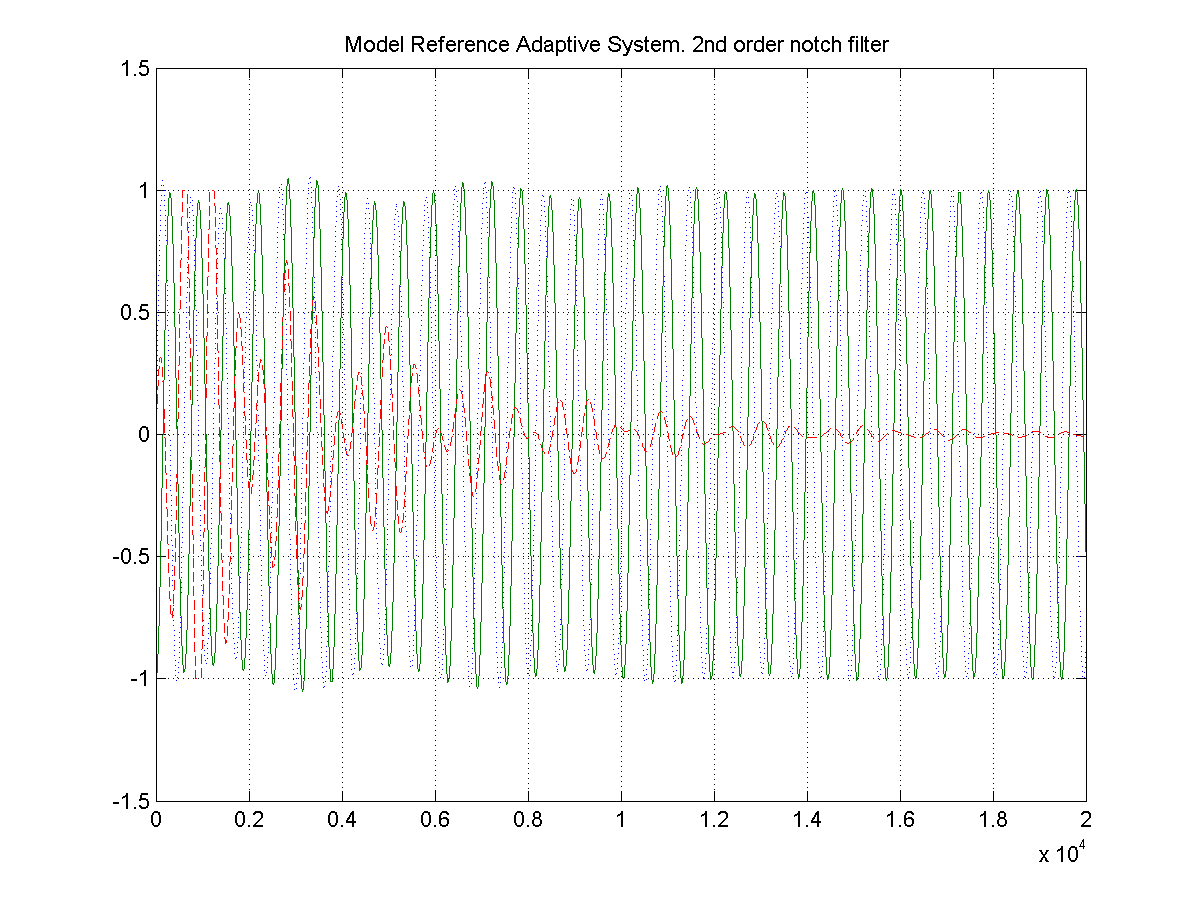
Wykres ponizej pokazuje przebiegi dostrajania przy zerowych stanach poczatkowych filtru, oczywiscie niezgodnych ze stanem ustalonym.

A ten pokazuje dostrajanie filtru adaptacyjnego przy niepoprawnej poczatkowej estymacie czestotliwosci.

% 1987 - Continous Time MRAC
% Model Reference Adaptive Control based on Lyapunow theory. Modern and very
% simple and effective adjustment rule origin from Lyapunow theory.
% 2'nd order notch filter for automatic rejection of base sine wave.
% Only noises and distortion remain (Red line on diagram, amplified by 5 times)
% on output
% th1 is gain-filter quality adaptation , th2 is a frequency adaptation .
% Arbitrary value od g1 (adaptation gain for th1)
% and g2 (adaptation gain for th2) can be used for stability.
% But response of course depend on g1 i g2 gain. So, optimal value occur
% Input is a clear sine wave (plus third harmonic). Explained later in
% Adaptacyjny filtr srodkowowzaporowy. J.Matusiak. III KKNT
% Przetwarzanie sygnalow w telekomunikacji, sterowaniu i kontroli, 1998 pp 153-155
% Adaptacyjny filtr srodkowowzaporowy. J.Matusiak, M.Durbas.
% XX Miedzyuczelniana konferencja metrologow, 1988 pp 230-234
%
N=20000; t=1:1:N; x=t; y=t; z=t; sp=0; dp=-1; b=0.1; th1=b; th2=1; e=0; a=0.01;
g1=0.1; g2=0.1;
% sp=wyjscie srodkowoprzepustowe filtru zmiennych stanu, Green Line on diagram
% sp=wyjscie dolnooprzepustowe filtru zmiennych stanu, Blue Line on diagram
% Reworked from TurboPascal
Przyklad = 'C'; % Wybor przykladow
switch(Przyklad)
case 'A'
sp=0; dp=-1; b=0.1; th1=b; th2=1;
% Stan ustalony filtru i estymat
case 'B'
sp=0; dp=1; b=0.1; th1=b; th2=1;
% Stan anty-ustalony filtru i ustalony estymat
case 'C'
sp=0; dp=-1; b=0.1; th1=b; th2=1.1;
% Stan ustalony filtru i rozstrojona czestotliwosc
case 'D'
sp=0; dp=0; b=0.1; th1=b; th2=1;
% Stan zerowy filtru i stan ustalony estymat
otherwise
end

for i=1:N
u=sin(i*a);%+0.1*sin(3*i*a);
dp=dp+a*sp;
sp=sp+a*(b*u-dp*th2-sp*th1);
e=sp-u;
th1=th1+g1*a*e*sp;
th2=th2+g2*a*e*dp;
x(i)=sp; y(i)=dp; z(i)=5*e;
if e>0.2 z(i)=1; end;
if e<-0.2 z(i)=-1; end;

end

plot(t,x,':',t,y,'-',t,z,'--'); grid;
title('Model Reference Adaptive System. 2nd order notch filter ');